Because I am fully cognizant that these musings betray an obsessiveness that may not be healthy, it is with some trepidation that I post these final thoughts on hang angles. For those who weary of the topic, take comfort in my promise that this is the final post on the subject for the immediate future.
In a previous post, I mentioned in passing that cant has an effect on hang angles. Before examining this effect, let us define cant and enumerate some of its purported benefits.
A canted saw is one whose toothline is not parallel to its spine. Invariably, the taper is such that the depth of cut is greater at the heel than at the toe. While some old saws have canted blades that are accidental byproducts of careless sharpening or rough handling, there is ample evidence that cant was an intentional feature on many early saws. While I know of no written evidence that shows early makers claimed any advantages for canted blades, modern writers and makers are not so silent. Four of the most commonly cited benefits are these:
- By changing the angle at which the teeth attack the fibers of the wood, the saw cuts more smoothly.
- By effectively raising the toe of the saw above the heel (at the toothline), the danger of cutting past the marked baseline on the backside of the board is lessened.
- By removing some of the plate, the saw is lightened and the center of gravity is shifted towards the handle. This is further enhanced if the back, or spine, of the saw is also tapered (as is common on many canted saws of old).
- It just looks cool. And it is nearly a universally accepted principle that, given two tools of identical functional quality, the one that looks better will almost always fare better in supposedly objective tests.
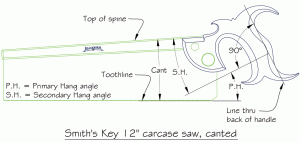
Before going further, let us first define three measurements. The first of these is cant, which we define as the angle formed between the toothline and the top of the spine. On an uncanted saw, this is 0 degrees. We call the second measurement secondary hang, and define it as the angle formed between the top of the spine and a line drawn perpendicular to the back of the handle. The last is primary hang, which we have heretofore simply called hang. In the trivial case of an uncanted saw, the primary and secondary hang angles are identical. The relationship between cant, primary hang, and secondary hang is shown in Figure 1, and is given by the equation:
secondary hang = primary hang – cant
To illustrate points 1 and 2, consider the uncanted saw in Figure 2, a typical twelve inch carcase saw with a primary hang angle of 33 degrees. The easiest way to add cant is by removing some of the metal at the toe of the blade. If we remove 1/2″, a cant of 2 degrees is introduced, increasing the primary hang angle of the saw to 35 degrees. The secondary hang angle remains unchanged.
Because the spine of a saw is so visually dominant while sawing, the natural inclination is to use it as a reference point when sawing, so it is reasonable to expect that both the canted and uncanted saws are held with their backs horizontal. This being so, the teeth of the canted saw are cutting with the grain rather than directly across it (Figures 3 and 4). While it certainly does not hurt, the benefit is is minor when ripping, and makes virtually no difference when cross-cutting. This covers the first of the reasons enumerated above.
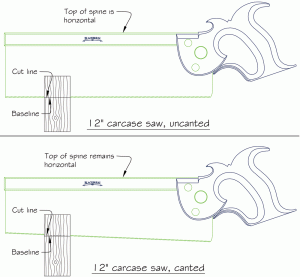
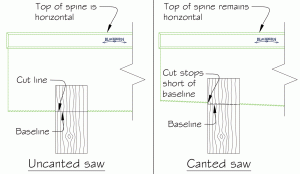
Figure 3. Top: Uncanted saw cutting a typical tenon cheek. Bottom: Canted saw cutting a typical tenon cheek. In both cases, it is presupposed that the back is horizontal.
Further examination of Figure 4 reveals the rationale behind the second reason. When the saw teeth reach the baseline of the cut in the front of the workpiece, they have not yet reached the baseline on the back (which is not visible whilst sawing), reducing the risk of overshooting your mark. To reiterate an important point, this benefit depends on the premise that the back, or spine, is always horizontal.
In the scenario outlined above, the handle is unchanged in its relation to the spine of the saw (the secondary hang angle). This means that the sawyer’s positioning, stance, and hold on the saw can remain unchanged even while the primary hang angle increases. Since the primary hang angle has increased, the transfer of the applied force to the teeth is (slightly) affected. The effects of this are discussed in great detail in two previous posts: Concerning (primary) hang angles and saw handles and Further discussion of (primary) hang angles.
If canting is accomplished by pushing the toe end of the spine down on the blade (as often happens with folded spines), then the secondary hang angle is decreased, affecting the sawyer’s positioning, stance, and hold on the saw (refer to Concerning (primary) hang angles and saw handles for more detail). The primary hang angle is unchanged, so the transfer of the applied force to the teeth is unaffected.
It goes nearly without saying that cant may be introduced by endless combinations of changes to primary and secondary hang. Exploration of these borders on tedium and would only tax our patience. [Border? I think that line was crossed long ago. -Ed.] I would hope that sufficient knowledge can be gleaned from this and prior posts to enable puzzling out the varied effects.
The third cited reason, the reduction of weight, has the effect of reducing the downward force provided by the weight of the saw itself. This will make the saw feel somewhat less aggressive, as the teeth bite into the wood a little less. However, this is countered by the increased primary hang angle (assuming the first scenario outlined above) that directs more of the applied force downwards. The degree to which the two offset each other depends on the amount of cant and weight difference, and can be more fully explored in the post Further discussion of (primary) hang angles.
In practice, I find the first of these reasons to be practically negligible, the second to have some merit, and the value of the third to be dependent on the preferences of the sawyer. In short, canting has a negligible to minor effect on the mechanics of sawing.
This leaves the fourth reason, the sheer awesomeness of the canted look, which needs no further explanation.



Very well reasoned Isaac. I also agree with your conclusions on the cited benefits that you mention. However, I think there is perhaps another potential benefit that you didn’t include in your analysis. It would be much easier to describe this with the aid of a couple of diagrams, but I hope I can convey the potential benefit in words alone.
What about the effect of cant on rake angle? If you take two saws with the same ppi and file one set of teeth with 0 degrees of rake and the other set of teeth with 5 degrees of negative rake, the teeth with a 5 degree rake angle would have a slightly deeper gullet. Also if you measure the area of the triangle between the teeth in each case, the teeth with a 5 degree rake angle would have a greater area and hence more space for the sawdust to collect. Now older saws were often filed with 0 degrees of rake and some were even filed with a positive rake angle to make the teeth cut even more aggressively. For those who wanted a more aggressive cutting saw, the cant angle turns a saw filed with 0 degrees of rake into a saw with positive rake when the spine is held horizontal. It is therefore a way of getting a positive rake whilst keeping the same area for the sawdust to collect that a 0 rake angle affords.
Hope that makes sense. Thoughts?
Andy,
I had some computer issues (and I needed some time to read through this). I think you are partially correct in your assertions.
The gullets are deeper, and have about 10% more space. Most of the time, I don’t think that is a really big deal, but it certainly does not hurt.
However, I don’t think it changes the effective rake angle, since the direction of travel is always parallel to the toothline. So, looking at the teeth before and after canting relative to a fixed perspective, such as the horizon, you would perceive a change in the rake angle (assuming the spine remains horizontal). But, when you begin cutting, the teeth in the canted blade will no longer travel parallel to the horizon, but at an angle that deviates from it by the degree of canting. In both cases, the relation of the teeth to the cut in the wood remains unchanged.
Is that a clear explanation of my reasoning?
Isaac
Yes perfect Isaac and you are of course right. Thanks.
When beginning this you mentioned this would be the “final post on the subject for the immediate future.” With the immediate future now behind us relatively, what else might you have to offer on the subject. I feel Hang to be the most important aspect to consider when approaching the construction of a new saw, with tooth geometry in correlation to the hang running tandem to this aspect. 99.9% of woodworking we do involves the inclined plane and you thoroughly discussed the math in prior posts, I suppose a good question might be “How do we find the sweet spot?” That magical combination where we no longer concentrate on the saw as it has been so well defined to become an extension of our hand. It is a loaded question I know, but one I think that deserves some exploration. Thanks Isaac for all the great info, keep it coming.
Brian, that’s a very complicated question to answer. I had, at one time, thought of trying to graph out a relationship between hang, rake angle, and several other variables such as type of wood, force required to cut, ease of starting, and skill level. It’s easy to design the experiments in my mind, but the time and effort required to carry the experiments out is daunting, particularly when compared to the payback. There’s really not a wide range of rake angles needed to cover almost every situation (and those vary from person to person, so it’s really difficult to draw broad focused conclusions).
Isaac